ALEX KAY BLOG

METRIC SPACE

We might have entities described by N-dimensional vectors so we can apply some other math abstractions effectively, but do we really know that we have only one way to calculate distances among the vectors? We are able to expand our assumptions on comparing operations to find differences and commons more effectively and even maybe faster!

Introduction

Long time ago, people introduce such terms as time and space. Both of them are transcendental and are used as abstraction to describe word around us. Such definition for this terms wasnt given by myself only, but we won't discuss it in this paper right now, but I recommend you to search this philosophy question by yourself.

When you design metrics to compare things, you are a lot more free in designing of it, you aren't restricted by the laws and nature principles, but you have to follow some simple rules which makes your systems comparable and scalable to other ones. And, as you already know, it is the topic of the paper.

History

People have been using the idea of metrics all the time they do the deal with them, but as metric spaces as discipline was introduced in 1906 by German mathematician Maurice Frechet. The discipline took an idea of topological properties which leads to the study of topological spaces.

Base definitions

Element (usually called point) - distinct object that belongs to set and have properties. In classical Euclidean geometry, an element is a primitive notion that models an exact location in the space.

Set - mathematical model for a collection of elements, which can be mathematical objects of any kind.

Metric (distance function, distance) - is a function that gives a distance between each pair of elements (point) of a set. The metric satisfies a few simple properties:

The distance from A to B is zero if and only if A and B are the same point
The distance between two distinct points is positive
The distance from A to B is the same as the distance from B to A
The distance from A to B is less that or equal to the distance from A to B via any third point C

Metric space - is non empty set together with a metric on the set.

Idea

Comparing object helps to defferentiate things we are working with. The quality and principles of comparing might help better descrive the system and introduce mathematical models. In comparing purposes, firstly, we must define properties we are working with and then define the way we leverage them. Common example of the properties list is N-dimensional vector which aggregates them, but it's not the only one way how to do this.

People used to think about metrics in terms of linear geometry distances. Also we may use metrics of other forms, for example such metrics as Levenshtein distance, which allows to measure the difference between to sequences. And there are a lot of others: Helly metric, Graph edit distance, descrete metrics, etc.

Usage examples

The common example of such distance - Euclidean distance which calculates absolute difference between two elements. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance.

Minkowski distance is a metric in a normed vector space which can be considered as a generalization of both the Euclidean and Mangattan distances. The Minkowski distance of the order p (p is an integer) between two points X, Y $$ {X = (x_1, x_2, ..., x_n), Y = (y_1, y_2, ..., y_n) \in \mathbb{R}^n} $$ Defined as: $$ {\displaystyle D\left(X,Y\right)=\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac {1}{p}}} $$

p = 2: Euclidean distance
p = 1: Manhattan distance
p -> inf: max(x_i, y_i)
p -> -inf: min(x_i, y_i)

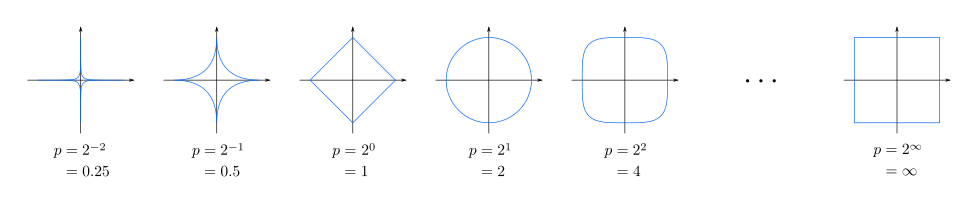
Levenshtein distance may also be referred to as edit distance, although that term may also denote a larger family of distance metrics known collectively as edit distance. It is closely related to pairwise string alignments. For example, the Levenshtein distance between "kitten" and "sitting" is 3, since the following 3 edits change one into the other, and there is no way to do it with fewer than 3 edits: